Goddelijke schoonheid in getallen*
Fred Pruyn
*Lezing in Middelburg, 6 oktober 2007.
Mocht u een probleem hebben met cijferen, dan kan ik u geruststellen. Getallen hebben mij ook altijd behoorlijk dwars gezeten. Ik was altijd de schandvlek van de wiskundeklas. Sommige sommetjes kon ik nog wel maken, maar als dan bij een examen werd gevraagd bepaalde stellingen te bewijzen, keek ik omhoog en vroeg me af of ik wel op de goede planeet was geland. Ik moest stellingen bewijzen, maar zag nergens bewijsmateriaal. Ik wist niet wat men van mij wilde. Ik kon gewoon niet communiceren met getallen, was als verlamd. Wiskunde was dan ook het vak waarvoor ik uiteindelijk nog net de troostprijs kreeg. Dus daar zat geen toekomst in. Wiskunde zag ik als een afwijking in deze wereld, als de onderkant van een ijsschots. Koud en glad en altijd onbereikbaar. Het heeft een eigen jargon, een eigen grammatica en eigen spelregels. En dus hoeft u nu niet te vrezen dat ik u ga bestoken met moeilijke formules.
Maar er zijn gelukkig ook mensen op deze planeet die wel vertrouwd zijn met cijfertjes. Sommigen tot in het extreme. Wie kent niet de film Rainman, met Dustin Hoffman als een autist in de hoofdrol. In die film waarin hij Raymond Babbitt speelt, weet hij precies hoeveel lucifers er in een doosje zitten en wat de uitkomst is van een onmogelijke rekensom. Maar we weten nu ook dat deze mensen niet alleen in Hollywood-studio’s rondlopen maar ook echt bestaan. Een van hen is Daniel Tammet. Een savant, een autist met het asperger-syndroom, een goochelaar met cijfers zonder daarvoor op school te hebben gezeten. Deze goed ontwikkelde autist heeft een boek geschreven en de Volkskrant (21 september 2007) heeft daaraan ruim aandacht besteed. Op een blauwe dag geboren is de Nederlandse titel. Hij ziet getallen als zijn vrienden. Zoals wij emoties koppelen aan geuren en smaken, zo koppelt Tammet emoties die voortkomen uit tal van oorzaken en gebeurtenissen aan getallen. Getallen zijn voor hem dan ook niet zomaar cijfers. Ze doen zich in zijn hoofd voor als kleuren, vormen, bewegingen en geluiden die zijn gekoppeld aan emoties.
Het getal 1 is voor Tammet een stralend helder wit, alsof iemand met een zaklantaarn in zijn ogen schijnt. Vijf is een donderslag of het geluid van golven die op de rotsen slaan. Zevenendertig heeft iets klonterigs als pap, terwijl negenentachtig hem doet denken aan vallende sneeuw.
Een stukje uit zijn boek: ‘Ik ben geboren op 31 januari 1979, een woensdag. Ik weet dat het een woensdag was omdat de datum me blauw bijstaat, en woensdagen zijn altijd blauw, net als het cijfer negen of het geluid van harde, ruziënde stemmen.’
Tammet is ook in staat in recordtempo nieuwe talen te leren. Om dit te bewijzen werd hij door de Britse Channel Five televisieomroep uitgedaagd om in een week IJslands te leren. Het IJslands wordt gezien als een van de moeilijkst te leren talen. Zeven dagen later verscheen hij op de televisie van IJsland en sprak in een interview vloeiend IJslands.
Maar het sterkste punt van Tammet is nog altijd zijn rekenvaardigheid. Hopeloos ingewikkelde sommen ziet hij in de leegte voor zich, en plukt daar ook de uitkomst uit, zonder daar al te veel moeite voor te doen. Al deze bijzonderheden kunnen we misschien zien als een bevestiging van het theosofische axioma dat de mens in feite alwetend is, alleen staat ons ‘ontvangststation’ als ik onze grijze massa zo mag noemen, niet goed afgesteld. Veel hiervan heeft te maken met onze persoonlijkheid en niets met onze genen. Als we een ander leven zouden leiden, zouden we tot hele andere prestaties in staat zijn, wat leert dat elke speciale vorm van leven leidt tot andere uitkomsten in ons bestaan.
Psychologen en neurologen schijnen te hebben ontdekt dat aanleg voor talen zich in de ene hersenhelft moet bevinden en de aanleg voor rekenen in de andere helft. Is het dan nog wel zo vreemd dat taal en cijfers elkaars spiegelbeeld zijn? Van de kabbalisten heb ik geleerd dat je getallen ook anders kunt interpreteren en waarderen, dat je ze anders kunt lezen. Letters hebben een bepaalde waarde en cijfers kun je weer uitdrukken in letters. Ze zijn uitwisselbaar.
Als we denken kunnen we dat op twee manieren doen, horizontaal en verticaal. Horizontaal denken, betekent denken met ons hoofd. Breinwerk. Hersenbrekers oplossen, organiseren. Dat kost kracht en aldus zijn we op een puur stoffelijk gebied bezig, op een aards vlak. Maar als we denken met ons hart, liefde voelen en geven, een impuls voelen om te hulp te schieten, denken we ook, maar dan zonder dat het noemenswaardige kracht kost. We leven op zo’n moment eigenlijk op een hoger niveau.
Hier ontdekken we de hiërarchie in de natuur, tenminste als we die eeuwig opgaande lijn zien van stenen, planten, dieren en mensen, en wezens boven die mensen, tot in het oneindige.
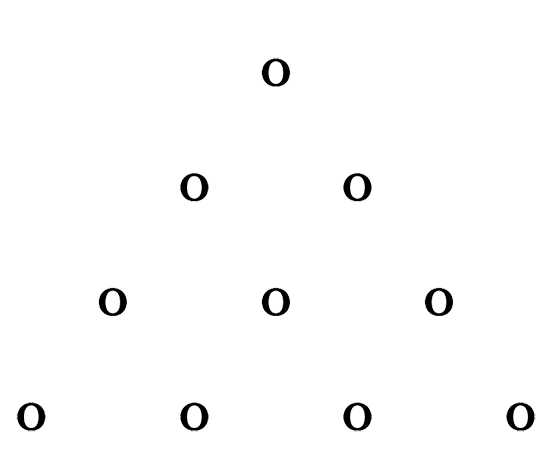De gedachte van hiërarchieën in de natuur werd door Pythagoras gesymboliseerd door zijn tetraktis. De tien punten die samen een gelijkzijdige driehoek vormen. Het is het tao, de alpha en omega, de 1 en 0 die samen de volmaaktheid uitdrukken. Ja, de tetraktis omvat alles. De getallen 1 tot en met 10. Het weerspiegelt het ontstaan van alles, de groei van elk ding, vanuit één punt naar beneden, naar zijn volwassenheid, maar ook de hiërarchie in de natuur; de natuurrijken die elkaar opvolgen. Het rijk van de mineralen aan de basis, dan het rijk van de planten, het rijk van de dieren, de mens en dan de onzichtbare rijken daarboven. In die volgorde treffen we deze leer ook vaak aan, terwijl dat eigenlijk de omgekeerde volgorde is. Beter zou zijn te zeggen goden, mensen, dieren, planten en mineralen, en nog veel verder omlaag naar de elementalen, de voor ons onzichtbare levensvormen beneden de natuurrijken van mineralen. Het idee van hiërarchieën in de natuur betekent dat er geen hoogste god noch een laagste duivel is. De hiërarchie strekt zich tot in het oneindige uit, er is altijd een voortgaande ontwikkeling, een eeuwige voortgaande groei in kennis en bewustzijn.
In de school van Pythagoras werd naast rekenkunde, sterrenkunde en meetkunde ook muziek bestudeerd, want muziek was de uitdrukking van getallen in een andere taal. Die muziek, of de getalsmatige verhouding, kon de verloren harmonie herstellen. Consonanten en dissonanten, Vishnu en Shiva, bouwers en afbrekers, samen werken ze aan een gezond organisme. Een overdaad van het een of van het andere zorgt voor een verlies van harmonie.
Pythagoras gebruikte zijn meetkunde zeker ook voor het vaststellen van akkoorden en de zuiverheid van muziekstukken. Maar voor de moderne mens zijn cijfers vooral belangrijk in de meetkunde. De meetkunde is in ons leven zo belangrijk omdat we alles vergelijken. Alles wordt vergeleken. Afmetingen, gewichten, afstanden, schoonheid, zelfs op moreel gebied. Iemand kan goed zijn, er is altijd weer iemand beter. Maar het is ook belangrijk om te weten in welk jaar we leven en hoelang een bepaalde cyclus nog duurt of kan duren.
Mathematica was al in de grijze oudheid een wetenschap. In de meeste talen is het woord voor wiskunde afgeleid van het Griekse woord máthima, dat wetenschap, kennis of leren betekent. Oorspronkelijk had de mathematica dus helemaal geen betrekking op wiskunde alleen. Het was de studie van de natuur die uitgaat van axioma’s of vooronderstellingen.
We kunnen ons misschien voorstellen dat dit heelal oneindig is, dat er geen einde is en geen begin. Dat is waar, er is immers nergens een grens aan te wijzen. Maar als ik zeg dat dit heelal een acht is, dan moeten we misschien even achter ons oor krabben. De acht, het universele symbool voor oneindigheid, is een geliefd en veel gebruikt symbool in de wiskunde en is te vinden op elk oculair van een verrekijker of microscoop. De 8 symboliseert de eeuwige en spiraalvormige beweging van cyclussen, die eindeloos doorgaan. Volgens Blavatsky wordt het gesymboliseerd door de Caduceus, de slang uit de esculaap van onze doktoren, en het regelmatig ademen van de kosmos.
De getallen 3, 4 en 7 noemt Blavatsky in haar meesterwerk De Geheime Leer (2:672) – en let op de volgorde – de getallen van licht, leven en eenheid. Het is de eenheid van zeven die onder andere is terug te vinden in de dagen van de week, en in de mens zelf. Het is een basis die we in alle godsdiensten terugvinden.
Langzaam maar zeker komen we dichter bij de bron van alles. Want de taal van de getallen leert ons onder meer hoe alles zich verhoudt, of iets in harmonie is, in evenwicht. Maar ook hoever we nog moeten gaan en hoeveel we al hebben afgelegd. Waar we vandaan komen en waar we naartoe gaan. Een van de grootste frustraties van de moderne mens is dat hij heimwee voelt naar zijn goddelijke thuis, maar dat niet weet maar onbewust wel registreert. Dat gevoel krijgen we bijvoorbeeld als we iets uit onszelf tevoorschijn brengen, als we creatief zijn en iets moois maken dat in evenwicht is, dat voldoet aan de gulden snede of phi (ϕ), een van de belangrijkste getallen of verhoudingen. Dan raken we die goddelijke wereld en zijn we eventjes thuis. Phi is de ‘ideale verhouding’, 1:1,618, en is terug te vinden in o.a. de vijfpuntige ster.
Niet alleen schilders en kunstenaars maken gebruik van de gulden snede, ook de natuur doet dat. In ruime mate zelfs. Ze is te zien in de spiraalvorm van schelpen zoals de nautilus. Veel planten groeien in deze verhouding en ook blijkt de mens volgens de studies van Leonardo da Vinci zo in elkaar te zitten. Maar het meest frappante is misschien nog wel dat het lijkt alsof de cijfers tot en met vijf nauw gerelateerd zijn met onze geestelijke wereld en alle hogere cijfers met de wisselvalligheden van ons wereldse bestaan.
Om iets hiervan te kunnen herkennen, moeten we ons wenden tot de Chinese filosofie van de I Ching, het Boek van Veranderingen. Daarmee zouden we intuïtief een idee moeten krijgen wat we in een bepaalde situatie zouden kunnen doen, laten we zeggen hoe we een dilemma kunnen oplossen. Het frappante van de I Ching is dat die draait rond de getallen 6, 7, 8 en 9. Het zijn afwisselend yin en yang-getallen, even en oneven, mannelijk en vrouwelijk. We vinden die tekens nu nog terug in de vlag van Korea.
Over even en oneven schreef Blavatsky in De Geheime Leer (2:685-6):
Omdat de monade [dat is, de eenheid die we ons van wat dan ook kunnen voorstellen] één is, en een oneven getal, noemden de Ouden de oneven getallen de enige volmaakte getallen; en beschouwden ze allemaal – misschien egoïstisch, maar niettemin als feit – als mannelijk en volmaakt, omdat ze van toepassing waren op de hemelse goden, terwijl even getallen, zoals twee, vier, zes, en vooral acht, omdat ze vrouwelijk waren, als onvolmaakt werden beschouwd, en alleen werden gegeven aan de aardse en helse godheden. In zijn achtste herdersdicht maakt Vergilius hiervan melding door te zeggen . . . ‘oneven getallen behagen god’.
Maar de pythagoreeërs beschouwden het getal zeven als een religieus en volmaakt getal. Het werd ‘telesphoros’ [vrij vertaald: ver schijnsel of ver licht] genoemd, omdat door dit getal alles in het heelal en de mensheid tot zijn einde, d.w.z. zijn vervulling, wordt gevoerd (Philo, De opificio mundi, §35). De leer van de sferen – vanaf de tijd van Lemurië tot aan Pythagoras – laat zien dat zowel de zeven krachten van de aardse en ondermaanse natuur, die onder het bestuur van de zeven heilige planeten staan, als de zeven grote krachten van het heelal, te werk gaan en zich ontwikkelen in zeven tonen, die de zeven noten van de toonladder zijn.
Dit is des te fascinerender als we deze kennis rond de trigrammen van de I Ching beschouwen in combinatie met de oneindige reeks van het getal pi (π, 3,14159...), de verhouding tussen de diameter en omtrek van een cirkel. We komen dichter bij onze goddelijke bron.
We zien dat pi niet alleen maar de wiskundige factor van technici is, die de verhouding probeert weer te geven tussen de omtrek van een cirkel en zijn middellijn, maar ook dat het de verhouding van het goddelijke weergeeft ten opzichte van de gemanifesteerde monade. De eerdergenoemde Tammet, het genie, ziet pi als het mooiste dat er is. Pi is een irrationeel getal, een getal zonder einde. Het is niet door mensen uitgevonden en heeft in alle tijden bestaan. Het is de goddelijke poort van leven en lijkt als symbool daarom misschien zoveel op de poort van de taoïsten. Het getal pi zonder komma (31415) wordt door Blavatsky de getalshiërarchie van de dhyani-chohans genoemd (GL 1:121). Bij de joden was pi altijd al gelijk aan de Alhim, ofwel God. Het is te vinden in de theogonie van Pythagoras waarin we een andere dan meetkundige verklaring voor dit raadselachtige getal vinden. Daarin ‘waren de hiërarchieën van de hemelse menigten en goden genummerd en werden met behulp van getallen uitgedrukt’.
Diogenes Laertius, zoals geciteerd door Blavatsky in De Geheime Leer (1:475), vertelt ons dat Pythagoras de esoterische wetenschap in India had bestudeerd, daarom zeggen zijn leerlingen:
De monade [de gemanifesteerde] is het beginsel van alle dingen. Uit de monade en de onbepaalde duade [chaos] ontstaan getallen; uit getallen, punten; uit punten, lijnen; uit lijnen, oppervlakken; uit oppervlakken, lichamen; hieruit vaste lichamen die bestaan uit vier elementen – vuur, water, lucht, aarde; uit al deze, getransformeerd [en in wisselwerking staand], en totaal veranderd, bestaat de wereld.
In het oeroude oosterse boek van Dzyan (‘kennis door meditatie’) wordt pi als volgt ‘half grafisch’ uitgelegd:
‘De grote moeder lag met de
, en de | , en het
, de tweede | en de
in haar schoot, gereed om deze voort te brengen, . . . van wie de twee ouders de
en het · (punt) zijn.’ – GL 1:476
Net zoals in veel andere oude kosmogonieën symboliseert ‘de grote moeder’ het allesomvattende Al. De grenzeloze oneindigheid, niet alleen op zintuiglijk gebied, maar ook daarbuiten. De eerste differentiatie, het eerste ontwaken, het eerste begin van heterogeniteit binnen de homogeniteit, is de punt in de cirkel. De punt breidt zich uit tot een lijn (|), de lijn breidt zich tweedimensionaal uit en vormt zo een vlak. De eerste driehoek (het eerste cijfer van π) is gevormd. Het Idee is er, de goddelijke gedachte. Het heeft alleen nog een voertuig nodig om zich te manifesteren. Dit is het vierkant, de 4, de combinatie van de vier elementen: vuur, water, lucht, aarde. Tevens het eerste driedimensionale platonische lichaam (tetraëder). Het Idee kan echter niet rechtstreeks in de stof werken, er is een scheidingsgebied, een niemandsland, tussen de wereld van de ideeën en de stof. Die afstand wordt voorgesteld door de |. Tegelijk kan de lijn de verbinding voorstellen tussen geest en stof, die in essentie één zijn.
Dus de geest (3) daalt af in de stof (4) en vormt aldus de mens (5).
De oneindige lange reeks cijfers die volgt op de 5 kan misschien symbool staan voor de oneindig verder-differentiërende of afdalende geest in de stof. Resultaat: een oneindige variatie aan levende wezens en hiërarchieën in de natuur.
We hebben gezien hoe uitzonderlijk mooi de wereld van de getallen kan zijn. En waarom getallen, maat en ritme thuishoren in een volmaakte wereld. Is het ook niet mooi om te zien hoe taal, getallen en muziek bij elkaar horen? Hoe het leven zich voor het grootste gedeelte afspeelt in de onzichtbare, abstracte wereld van de geest? Als we de tijd en gelegenheid nemen om te mediteren of na te denken over pi, phi en het universum zullen we eerder zien hoe alles deel uitmaakt van één gigantisch organisme, waarin alles een eigen plaats heeft, maar toch ook weer deel uitmaakt van al het andere.
Andere artikelen over wetenschap: wiskunde